Heatsink Calculations and Efficiency Theory

[Cyparagon]

Copper also has a higher heat capacity than aluminum, meaning it takes more energy to raise the temperature of one kg of copper 1 degree than it does for aluminum.

But copper is more dense, and therefore has more mass per unit volume. Our applications are generally limited by volume, and the heat capacity is actually about the same per unit volume.

The thermal conductivity of most aluminum alloys is around 100-130W/mK

You mean to say an alloy of aluminum is half as conductive as pure aluminum? That's a rather large difference for such a small change in material. Source?

copper will distribute the heat evenly through the heatsink 4 times faster than an aluminum heatsink.

That's a bit misleading since the heat isn't created all at once. If you actually take the temperature of various parts of aluminum, it's virtually all the same. Take this image of the arctic for example. The junction of the tail cap provides FAR more resistance than even several inches of aluminum. If it were made of copper, the image would not be much different

 

[Pontiacg5]

But copper is more dense, and therefore has more mass per unit volume. Our applications are generally limited by volume, and the heat capacity is actually about the same per unit volume.

A heatsink made of copper will have a greater mass than an aluminum heatsink the same size. Weather or not that difference in mass is significant depends on the size of the heatsink. True, if you are staying small enough the difference may not be as much but there will be a point where copper would have more thermal capacity per unit volume than aluminum. When I get home I will pull up a few heatsink models and post the mass of certain heatsinks in aluminum and copper. (say a C6 aluminum and copper heatsink.) I believe that even in a heatsink so small the difference in mass between aluminum and copper is pronounced enough that the copper heatsink will still have a higher overall thermal capacity.



You mean to say an alloy of aluminum is half as conductive as pure aluminum? That's a rather large difference for such a small change in material. Source?

I don't have a link for each source, but if you google thermal conductivity of aluminum **** you should get MSDS results that will confirm what I am saying.

The thermal conductivity of 6061, the material most likely to be used is 160W/mK, 6063 (another candidate, more expensive but better to anodize.) is 200W/mK. 7075, a structural aluminum probably not used in lasers much due to cost is 130W/mK. These numbers will change depending on the temper of the aluminum as well.



That's a bit misleading since the heat isn't created all at once. If you actually take the temperature of various parts of aluminum, it's virtually all the same. Take this image of the arctic for example. The junction of the tail cap provides FAR more resistance than even several inches of aluminum. If it were made of copper, the image would not be much different

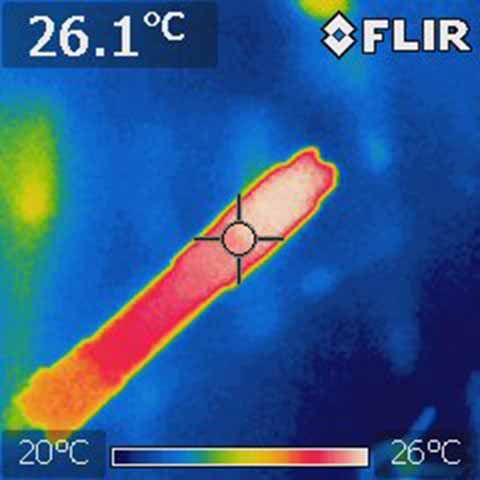
This picture confirms what I am saying is true. There is a clear difference in temperature between the head and body of the host so the temperature between one material (aluminum here) is not the same all the way through. Sure, it's not much but it is there. If the arctic was made of copper the difference in temperature would be less pronounced.

Also, the heat is created all at once. As soon as that diode turns on it is wasting energy, that energy is distributed through the host as heat. As long as the diode is running at a constant current it will make (close to) the same amount of waste heat every second.

A video of the arctic running from room temperature would show similar results, the head would get hot before the body did. If you used copper the body would heat up faster than the aluminum since copper's thermal conductivity is that much higher than aluminum.

f i v e

 

[Isoleucine]

Cyparagon, sorry for me being a bit subjective... I didn't want to do another run on math, so I just estimated. Copper does have a greater potential at being a heatsink, and thus, it will be able to move and groove the heat around better. Perhaps Im probably wrong about temperature, but I am SURE that it will be able to last longer in terms of operation.

 

[Cyparagon]

In terms of volume, or in terms of mass?

 

[Benm]

I guess the major error is to consider a heatsink as a thermal mass that does -not- conduct heat to ambient. Obviously the point of any heatsink is to transfer heat from a component to ambient, not to just sit there as a block getting warmer.

This is also where the idea that copper is much superior than aluminium comes from. Copper does have a slightly better thermal conductivity, but it has a huge volumetric energy density compared to aluminium.

In a real world, steady state, situation there is virtually no difference between copper and aluminium, since the exchange of heat between the heatsink and ambient is the limiting factor. If you were to make two identical heatsinks, one from copper and the other from aluminium, you'll find the performance almost identical in any setup that runs for infinity.

 

[Isoleucine]

I mean comparatively with the aluminum. It will be able to run a bit longer.

Also BENM, what if you finned a heatsink to increase its surface area?

 

[pullbangdead]

No need to reinvent the wheel with respect to this thermal conductivity vs. heat capacity trade-off.

It's called thermal diffusivity: the thermal conductivity divided by the volumetric heat capacity.

You mean to say an alloy of aluminum is half as conductive as pure aluminum? That's a rather large difference for such a small change in material. Source?

Alloy scattering has a large effect.

 

[Isoleucine]

A large group of people do not know how to calculate this. I, did. Proudly. But still with a bit of errors.

 

[chipdouglas]

I mean comparatively with the aluminum. It will be able to run a bit longer.

Also BENM, what if you finned a heatsink to increase its surface area?

it depends where you want to use it... in a labby yes, as a drop in heatsink in aflash light, no.


michael.

 

[foulmist]

I think you should make a simple calculator for heatsink's mass/size etc with given diode and current applied would be great because I didn't get most of the stuff here I couldn't even read it my brain started hurting

 

[rhd]

I think you should make a simple calculator for heatsink's mass/size etc with given diode and current applied would be great because I didn't get most of the stuff here I couldn't even read it my brain started hurting

My standing offer to the forum is that if someone will simplify the math (in the sense of turning the math into a few formulas, or an algorithm), and if the actual task is somewhat helpful to the laser community, then I'll take the time to make any web tools that are useful

 

[Wolfman29]

I would, except the forumulae are really nasty and involve lots of differentials... especially because there are so many variables like whether or not there are fins, how big the fins are, etc.

 

[Isoleucine]

HERE IS A SIMPLIFIED VERSION OF THE OP! ... Since I got bored, and helping a community is super cool IMO.

Assume the Following - aka Ideal Conditions so that things dont get complicated.
-No heat escapes the heatsink in any way, shape, or form.
-Infinite Time is given for the diode to conduct heat on a per second basis
-Conductivity of Metals is Omitted
-And Metals are 100% pure.

Here is the Equation for how much heat is GENERATED.

Imput wattage (volts x amperes) - laser power output = heat generated, i.e wasted energy

for example. A 445 diode under typical conditions. Substitute your values accordingly

4.5 watts of power ( or 4.5V and 1amp) - 1W = 3.5Ws of heat.
____________________________________
Next, use the equation to calculate heat

Q = (specif. heat value of metal in grams) (mass in grams) (change in temp, final temp minus initial in centigrade)
With this, we can find out several things. How long it takes for something to heat up and how much heat will be generated under typical operation.

EXAMPLE
specific heat of Aluminum is .900 exactly
specific heat of copper is .385 exactly
I have an aluminum heatsink...

To find the amount of energy it takes to heat up to a certain temperature
Q = .900 x 20 x 40
Q = 720joules.
1 watt is 1 joule per second.
3.5 joules of heat are generated per second.
720 / 3.5 = ~205 seconds for it to heat up 40 degrees centigrade, or 3 minutes and some.

To find the amount of heat generated after T seconds.
Q = .9 x 20 x (change in temperature)
Q is equal to joules. watts is joules per second.
I will run it for TWO minutes.
120 x 3.5 (joules generated per second) = 420 joules total generated.
going back to the equation

420 = .9 x 20 x (change in temperature)
(420) / (.9 x 20) = change in temperature
420 / 18 = 23.333 ...

So If I run it for 2 minutes, it should heat up by ~23 centigrade under normal conditions.

_____________________
If you cannot understand this at THIS point, you can be deemed less intelligent than an eighth grader. This JUST substituting values in equations and solving for the unknown.

Furthermore, know that this is UNDER THE WORST CONDITIONS POSSIBLE, that is, no heat escapes the heatsink. Heatsinks will last longer than this, but this is the basic idea of a DUTY cycle. Should run no longer than the calculated time for a long life on a diode. also... the heatsink should not reach temperatures greater than 140F OR 60C. IMO. If it does get to that temperature, it should be very hot to the touch. have a nice day.

 

[Wolfman29]

A couple of things....

1) Don't call people stupid. You sound like an arrogant a$$hole when you do that, and only I'm allowed to do that. Jokes aside, I would suggest being a bit more friendly. Not everyone is great at math.

2) Your equations are not necessarily true at all. They are *ONLY* true if the die of the diode is chemically bonded to the actual heatsink and it is assumed that the surface area of which they are touching is infinite. Basically, you didn't include how long it takes the heat from the die of the diode to get to the heatsink, and that number is going to be pretty damn high - there are three junctions, all of which DECREASE heat conductivity - die to diode casing, diode casing to Aixiz module, and Aixiz module to heatsink. Because none of those will be instantaneous distributions of heat, you will find that, while the heatsink may be +20 degrees C, the Aixiz module may be +25 degrees, the diode may be +30, and the die may be +35 degrees (random numbers, but the point should still be clear).

The point of the matter is that it's not this simply. You have to calculate how good the junction transfers are.

 

[Isoleucine]

I guess so... for 1.

The point I'm trying to express here is that these are under ideal conditions. My opinion for the temperature limit only merely implies the limitations of the more internal components. Press fit heatsinks tend to conduct heat better, but thats a rather different story, as I am using that sort of stuff. This is the bare minimum anyone can understand without utilizing calculus, additional variables, and even more functions. If I did as such, people would have a rather difficult time doing this experiment on their own time.

I understand that complexity is a must, but this is not a thermodynamic analysis lab write up. Its simply what I know, and ways it can be utilized for the betterment of the community. These are only for simplicity's sake.

 

[Wolfman29]

Well, yes. But the point is, by posting that, you are giving people hope that they can safely run their laser for that amount of time (at the maximum). The point being, if you consider everything I mentioned, you will probably result in a decrease of 50% or so (once again, random number, but it seems likely).