amkdeath said:
so jsut a question... at 400mA a .5W pot with no resistor in parallel with it would hold?
You can calculate power dissipated by a resistor by:
1. P = I^2 * R
2. P = V^2 / R
For regulators with a reference voltage of 1.25V, such as the LM317, MC33269, and LM1117 series:
With a series resistor to limit to 400mA, it would need 3.125ohms effective resistance when the pot is turn all the way down (close to 0 ohms). The shunt resistor voltage (across the resistor/pot) will be 1.25V, so P = 1.25^2 / 3.125 = 0.5W. That is the power dissipated by the equivalent resistor (resistor and pot combined), so the pot and the resistor in series would be dividing the power, but not equally depending on the resistance of the pot. You can calculate the power dissipation at a given current by knowing what the pot resistance is at that current and using the first equation above.
I came up with this little equation that you can graph to figure out the power dissipation of your pot across a range just by plugging and chugging ;D
Power(pot) = ((1.25V / Iout) - Rseries) * Iout^2
I'm not sure it's entirely accurate, but I think it should work. The calculated peak power dissipation for the pot is around 1/8W at ~200mA assuming a 3.1ohm Rseries, so at higher and lower currents (for the same Rseries), the power dissipation drops as either the current drops, or the pot has less resistance than the Rseries.
From what I have read, as operating temp increases, effective power handling of a resistor goes down (manufacturer's datasheet may say something about how much or at least give a max temp), so at least doubling the the effective resistance of the pot is a good idea, but the fixed resistor should be OK as long as it's rated near the peak output, which for 400mA will be when the pot is turned to [near] zero ohms and will be close to 0.5W.
[Added 5/20/2008]
So you basically want to calculate what the power dissipated by the pot is at a certain current output. What happens is that when you put a resistor in series with another, it's additive for resistance and power. But if the resistors are not equal in their resistance the distribution of power between them is unequal (one will have more than the other). Since the pot changes it's resistance, this balance also changes as you adjust it.
So, for example, if you're pushing 1A through two series resistors that are 10 ohms each, the effective (combined) resistance is 20 ohms and the effective power disspation is 20W. But, you can calculate the power disspation of each as being 10W (
I^2 * R). So, by putting two 10ohm resistors in series, you can spread that 20W of power disspation out over two resistors rather than having a single 20 ohm resistor handle all 20W.
With the regulator, since current and resistance are changing, but voltage remains constant, it's a little more complicated. Basically what's going to happen is that the resistance of the series resistor will remain constant, while the pot will change (obviously), but as the combined resistance decreases, current output from the regulator (and thru the resistors) increases. As current increases the power dissipated also increases, and since both the pot and the resistor have the same current being pushed through them (since they're in series), the one with the higher resistance will have the most power dissipated (think of the P =
I^2 * R, where bigger R equals more power).
The peak of the current output will be where the pot and the series resistor are equal, ie where the combined resistance is twice that of the series resistor (2*Rseries). So you could actually simply calculate the peak power dissipation for the pot by:
1. (1.25/(2*Rseries)), which gives the output current (
I) of the regulator at where the pot is peaking in dissipation.
2. Then to calculate the power, you have to do
I^2 * R, so you square the above equation (which gave you
I) and multiply by the resistance of the pot, which Rpot = Rseries, so the equation for power becomes:
(1.25/(2*Rseries))^2 * Rseries
This is different from the equation that I posted before in that you're calculating the peak power of the pot needed for the current output limit you want (the top of your output range, determined by Rseries). The one I gave you previously in the post just gives you the power at a specific current setting for the regulator, so you can see what the power disspation would be at any point in your range of the pot's resistance.
[end added portion]
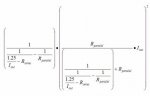
And then you have my parallel pot with resistor and series resistor that I'll be using on my adjustable driver, also called a star configuration, which to calculate the power dissipated by the pot requires a MUCH more complicated equation, which you can check out in the attached pic.
Someone please correct me if any of this is wrong as it's all stuff I derived from standard equations, not something I found online.