- Joined
- Sep 12, 2007
- Messages
- 9,399
- Points
- 113
What you need:
Meter stick or Tape measure (metric preferred)
Diffraction grating with known line density*
Calculator
Laser
*If you don't know the line density of your grating, you can find it within ~.5% later on if you have a known stable wavelength (like green).
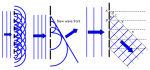
The concept of diffraction is based on the wave nature of light. Waves interfere to create new wave patterns. Here's a brief overview.

The distance between the waves (lineAC) is the wave length. Basic geometry will show that the two θ shown above are equal. Trig shows us:
sinθ = (lineAC)/(lineAB)
sinθ = λ/d
λ = dsinθ
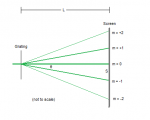
But since the angle is difficult to measure directly, we will use the projection of the pattern and trig.

tanθ = S/L
θ = arctan(S/L)
So what does all this mean? It means if we have the distance between the grating slits, the distance to the screen, and the distance between diffraction orders, we can find the wavelength!
λ = dsin(arctan(S/L))
"How important are units?" This equation only works if all the units agree, so best to convert everything to meters. That means your wavelength will show up as something like 0.000000658. Don't panic, this equals 658 * 10^-9. Recall that the SI prefix for 10^-9 is nano
"But Cy, my grating says 1000 lines/mm! What does that mean?" 1000 lines/mm is 1000000 lines/m. If we take the inverse, we have .000001 m/line (1µm spacing)
"And what if I don't know the line spacing?" You can find it, but you need a known stable wavelength (Pretty much anything that isn't a laser diode such as DPSS or gas lasers). Set everything up and take the two measurements. You have all variables except the line spacing. We can rearrange the equation to get d = λ / sin(arctan(S/L))
"Cool! So how accurate is this in practice?" Well it depends on how accurate your measurements and alignments are. Even if you do everything perfectly, there is still the variation in the grating itself. For best results, have the laser perfectly perpendicular to both the screen and grating, and have the screen far away - at least a meter. When I set this up, I found it was accurate to ± 4nm compared to my calibrated CCD spectrometer, but it was done on the kitchen floor with film grating and a floppy tape measure. Your results will vary. I don't want to see anyone claiming their laser is 657.23981247293847 nm like some people like to do with divergence. Your ruler is not accurate enough to have that many significant figures At least round to the nearest nm. It is also advisable to indicate an error margin, since it may be rather large. But if nothing else, it's a fun experiment
At least round to the nearest nm. It is also advisable to indicate an error margin, since it may be rather large. But if nothing else, it's a fun experiment 
Let me know what you think. Post your results! :beer:
edit: rhd made an applet if you don't have a calculator: http://rohanhill.com/tools/FindWavelength/
Meter stick or Tape measure (metric preferred)
Diffraction grating with known line density*
Calculator
Laser
*If you don't know the line density of your grating, you can find it within ~.5% later on if you have a known stable wavelength (like green).
The concept of diffraction is based on the wave nature of light. Waves interfere to create new wave patterns. Here's a brief overview.
The distance between the waves (lineAC) is the wave length. Basic geometry will show that the two θ shown above are equal. Trig shows us:
sinθ = (lineAC)/(lineAB)
sinθ = λ/d
λ = dsinθ
But since the angle is difficult to measure directly, we will use the projection of the pattern and trig.
tanθ = S/L
θ = arctan(S/L)
So what does all this mean? It means if we have the distance between the grating slits, the distance to the screen, and the distance between diffraction orders, we can find the wavelength!
λ = dsin(arctan(S/L))
"How important are units?" This equation only works if all the units agree, so best to convert everything to meters. That means your wavelength will show up as something like 0.000000658. Don't panic, this equals 658 * 10^-9. Recall that the SI prefix for 10^-9 is nano
"But Cy, my grating says 1000 lines/mm! What does that mean?" 1000 lines/mm is 1000000 lines/m. If we take the inverse, we have .000001 m/line (1µm spacing)
"And what if I don't know the line spacing?" You can find it, but you need a known stable wavelength (Pretty much anything that isn't a laser diode such as DPSS or gas lasers). Set everything up and take the two measurements. You have all variables except the line spacing. We can rearrange the equation to get d = λ / sin(arctan(S/L))
"Cool! So how accurate is this in practice?" Well it depends on how accurate your measurements and alignments are. Even if you do everything perfectly, there is still the variation in the grating itself. For best results, have the laser perfectly perpendicular to both the screen and grating, and have the screen far away - at least a meter. When I set this up, I found it was accurate to ± 4nm compared to my calibrated CCD spectrometer, but it was done on the kitchen floor with film grating and a floppy tape measure. Your results will vary. I don't want to see anyone claiming their laser is 657.23981247293847 nm like some people like to do with divergence. Your ruler is not accurate enough to have that many significant figures
Let me know what you think. Post your results! :beer:
edit: rhd made an applet if you don't have a calculator: http://rohanhill.com/tools/FindWavelength/
Attachments
Last edited: