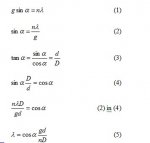dr-ebert
0
- Joined
- Mar 8, 2009
- Messages
- 710
- Points
- 0
3 weeks ago I bought a couple of these diffraction glasses from Alexzupinhea. After they arrived, I played around with them a bit and came up with two simple-to-do experiments which may have some practical merit for one or the other. The first one is on how to check your lasers wavelength. The second one is a qualitative assessment of fluorescence spectra.
If you shine your laser through these glasses, the single dot gets split into multiple dots, depending on the line pattern of the diffraction glass. With just vertical lines, you'll get a horizontal series of dots. With a criss-cross set of lines, you'll get a 2-dim array of dots, as seen in Alex' picture in the first post. For the reasons why this happens, check Wikipedia or your favorite physics textbook.
Here are some basic diagrams and formulas:
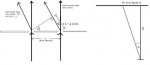
You get an nth-order diffraction spot when the path length difference between two adjacent slits in the grid is n times the lasers wavelength. See the right-hand part of the following picture. On the left-hand part, you see how the diffraction by an angle shows up as a projection against a wall: if the wall is at a distance D, the diffracted spot will be displaced by distance d from the primary beam.
We now have the necessary formulae. Let's transform them a bit.
d and alpha depend on the wavelength lambda, the other values D and g are independent. If we make the measurement for two wavelengths lambda1 and lambda2, we get two measurements for the spot distance, d1 and d2. Dividing, we get:
Next I shone various laser beams through the glasses and measured the distance of the (horizontal) first-order diffraction spot from the primary (undiffracted spot). With D=480cm, I got the following values for d using a green, red and violet laser:
d(green) = 52.7 cm
d(red) = 65.8 cm
d(violet) = 40.3 cm
Assuming that the 532nm wavelength for the DPSS green is the most reliable, and plugging the values into formula (7), we get this result:
wavelength(red) = 662nm
wavelength(BR) = 408nm
None of the measurements were done with any attempt at great precision. Still, the results are obviously within 1%, showing that the method is workable.
Note that the cos terms, and especially their fraction, is very close to unity, so in an approximation, it can be ignored. Also note that the spot deviations, d, in millimeters, are close to the wavelength in nanometers. If the projection distance had been 486cm instead of 480cm, the correspondence would have been nearly perfect, allowing the direct reading-off of an unknown wavelength.
Here's a picture of the three lasers shining through the glasses at the same time, aligned such that the primary spots overlap, thus showing the different amount of diffraction for the various colors. (The picture isn't too good, as my cellphone camera isn't very suitable for dim light conditions).
If you shine your laser through these glasses, the single dot gets split into multiple dots, depending on the line pattern of the diffraction glass. With just vertical lines, you'll get a horizontal series of dots. With a criss-cross set of lines, you'll get a 2-dim array of dots, as seen in Alex' picture in the first post. For the reasons why this happens, check Wikipedia or your favorite physics textbook.
Here are some basic diagrams and formulas:
You get an nth-order diffraction spot when the path length difference between two adjacent slits in the grid is n times the lasers wavelength. See the right-hand part of the following picture. On the left-hand part, you see how the diffraction by an angle shows up as a projection against a wall: if the wall is at a distance D, the diffracted spot will be displaced by distance d from the primary beam.
We now have the necessary formulae. Let's transform them a bit.
d and alpha depend on the wavelength lambda, the other values D and g are independent. If we make the measurement for two wavelengths lambda1 and lambda2, we get two measurements for the spot distance, d1 and d2. Dividing, we get:
Next I shone various laser beams through the glasses and measured the distance of the (horizontal) first-order diffraction spot from the primary (undiffracted spot). With D=480cm, I got the following values for d using a green, red and violet laser:
d(green) = 52.7 cm
d(red) = 65.8 cm
d(violet) = 40.3 cm
Assuming that the 532nm wavelength for the DPSS green is the most reliable, and plugging the values into formula (7), we get this result:
wavelength(red) = 662nm
wavelength(BR) = 408nm
None of the measurements were done with any attempt at great precision. Still, the results are obviously within 1%, showing that the method is workable.
Note that the cos terms, and especially their fraction, is very close to unity, so in an approximation, it can be ignored. Also note that the spot deviations, d, in millimeters, are close to the wavelength in nanometers. If the projection distance had been 486cm instead of 480cm, the correspondence would have been nearly perfect, allowing the direct reading-off of an unknown wavelength.
Here's a picture of the three lasers shining through the glasses at the same time, aligned such that the primary spots overlap, thus showing the different amount of diffraction for the various colors. (The picture isn't too good, as my cellphone camera isn't very suitable for dim light conditions).
Attachments
Last edited:
looking forward to it though! I love laser related formulas and plan on making a small notebook filled with any and all related data.
