What actually occurs with color blending?

[IsaacT]

Okay, so I have been curious for awhile now as to the relationship between colors of lasers when blending. Is there a formula for it? Also, how much does the process differ from say blending crayons? I imagine in theory it would be the same, since the colors we perceive are still caused by the light being reflected back at us, correct?

So I guess I am just trying to figure out why Blue+Red=Purple.

If

405___445_____532______660___

is the Spectrum of visible light, with 405 modeling an approximation of purple, 445 modeling and approximation of blue, 532 as a marker, and 660 modeling red, then why does 660 blended with 445 add up to something like 405?

Do the wavelengths shorten when combined? Maybe the waves interfere with each other and cause a shorter wavelenght as a result? Any explanations would be GREATLY appreciated!

Peace,
Isaac

 

[magonegro]

Wavelengths never change, it's just you retina that gets that color to your brain. Look here: Color vision - Wikipedia, the free encyclopedia

 

[Jaseth]

Blending crayons and blending light is very different. The colours we see daily (green grass, blue car, red mail box) are the result of the combination of different wavelengths which are left after being reflected by the material. As such, these colours are made by taking white light with wavelengths from all over the spectrum and subtracting some of them.
Combining laser light is an additive process as you add more light with more wavelengths.

As magonegro said, the wavelengths themselves do not actually change - a 532nm together with a 660nm laser (green and red) will appear to be yellow which is in between the two wavelengths, but in reality the 532nm and 660nm waves are still separate and not "true yellow" which may be for example 593.5nm.
Combining two wavelengths will always result in what appears to be a wavelength in between. Therefore, red+green can never become blue or violet, violet+blue can never become green, yellow or red, etc.

Seb

 

[pullbangdead]

Your eye has "red", "blue", and "green" cones. A green photon stimulates the green cone, so you see green; a red photon stimulates the red cone so you see red, etc.

Yellow photons stimulate both the red and green cones, so you see yellow, Your eye/brain is calibrated such that if both the red and green cones are being stimulated, the color you see is yellow. Therefore, if you stimulate both your red and green cones separately, using red and green light, your brain will see it as yellow, because that's how yellow light interacts with the cones in your eye.

And as said, light combines through additive color mixing. Crayons and paint combine through subtractive color mixing. You can look up color wheels for both situations online. But also be aware that computer monitors can't reproduce all the colors that your eye can actually see, so any images that are depicting color are only approximations.

 

[IsaacT]

As magonegro said, the wavelengths themselves do not actually change - a 532nm together with a 660nm laser (green and red) will appear to be yellow which is in between the two wavelengths, but in reality the 532nm and 660nm waves are still separate and not "true yellow" which may be for example 593.5nm.
Combining two wavelengths will always result in what appears to be a wavelength in between. Therefore, red+green can never become blue or violet, violet+blue can never become green, yellow or red, etc.

Seb

Your eye has "red", "blue", and "green" cones. A green photon stimulates the green cone, so you see green; a red photon stimulates the red cone so you see red, etc.

Yellow photons stimulate both the red and green cones, so you see yellow, Your eye/brain is calibrated such that if both the red and green cones are being stimulated, the color you see is yellow. Therefore, if you stimulate both your red and green cones separately, using red and green light, your brain will see it as yellow, because that's how yellow light interacts with the cones in your eye.

And as said, light combines through additive color mixing. Crayons and paint combine through subtractive color mixing. You can look up color wheels for both situations online. But also be aware that computer monitors can't reproduce all the colors that your eye can actually see, so any images that are depicting color are only approximations.

So while Red+Blue=Purple in Crayons, 660+445=552.5 since your brain registers the two colors it receives as one middle of the way wavelength? I realize it might not be exactly 552.5. Since the eye's sensitivity for color peaks at 555nm, it would indicate to me that the cone for green is stronger than the others so it might be any wavelength between the two.

 

[chipdouglas]

if you blend rgb with light you get white. if you blen rgb with crayons you get a funky nasty blackish color

michael

 

[pullbangdead]

So while Red+Blue=Purple in Crayons, 660+445=552.5 since your brain registers the two colors it receives as one middle of the way wavelength? I realize it might not be exactly 552.5. Since the eye's sensitivity for color peaks at 555nm, it would indicate to me that the cone for green is stronger than the others so it might be any wavelength between the two.

Don't think of it as a color line with violet on one end and red on another, think of it as a color wheel. So take your line, roll it up, and you find blue and red next to each other, and between them you find purple. Red + blue = purple. Red + green = yellow. Blue + green = cyan.

Additive color mixing, like combining light:

Subtractive color mixing, like mixing paint:

 

[IsaacT]

So it is all in our head, huh? When I look at yellow, I see yellow, but when I look at a mixture of Red and Green light, I perceive yellow, but am actually viewing Red and Green, just at the same time at the same spot in my vision.

 

[Gryphon]

^ you are correct, the same happens when we "see" magenta when 660 and 405 are combined

 

[IsaacT]

hmm.....I wonder if there is a formula that takes into account the average sensitivity of the different cones so that you can just plug in the wavelengths/power you want to mix and it will spit out the resulting wavelength....

 

[pullbangdead]

hmm.....I wonder if there is a formula that takes into account the average sensitivity of the different cones so that you can just plug in the wavelengths/power you want to mix and it will spit out the resulting wavelength....

Haha, yes, there is...but it's a bit more complicated than just "a formula". There is an entire mathematical framework built upon the theory and science of color perception in the human eye, and the approaches used today have been developed literally over the last 80+ years (the first big publication was the basis for the commonly-used CIE chart, the one you see if you google image search for "CIE chart", published in 1931***). The result is a set of color matching functions (there are actually different sets of functions now, some more commonly used than others). The 1931 stuff is still the easiest to "see" without doing more work, but the later stuff makes more sense once you get into it and is more accurate/representative.

For the quickest way to get at it yourself without having to take days to learn all of it, just go download a program called Chroma. It was made by a PhotonLexicon forum member named Tocket, here's his post about it on PL: Chroma - a laser color blender. Chroma does what you want: you put in monochromatic light sources with set powers, and it shows you where that mix of colors would fall on the 1931 CIE chart. Keep in mind the CIE chart is still very approximate though, because computer monitors are incapable of reproducing all the colors on the chart. Any given monitor can only reproduce colors within a small triangle on the CIE chart, not the whole thing, so what you see on the chart is just a representation/approximation of the colors, but it gives you the idea.


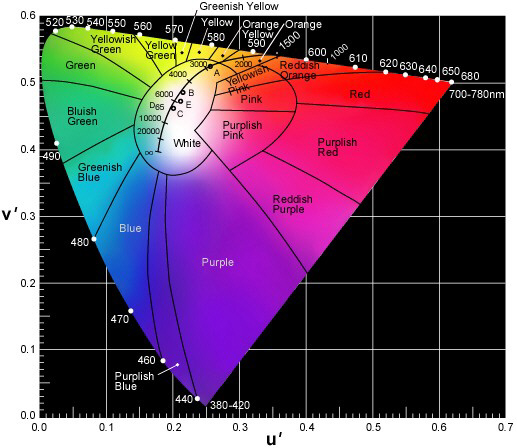
***Actually, if you just google image search for "cie chart", you'll see the more common 1931 CIE chart, and the newer/better/but more complicated 1975/1976 CIE chart. The 1931 is "taller" and has axes of x and y, while the later one is more short and wide, with axes of u' and v'. Here's a good version of the 1976 chart:

Basically, around the edges you see monochromatic wavelengths. Combining 2 wavelengths, by varying the power ratio you can reproduce any color on the straight line between those 2 wavelength. This is why white LEDs can be made with simply a blue LED and a yellow phosphor, it comes out white (although there are other problems, like color reproduction, as in shining white light made by blue+yellow will look white on a white surface, but won't look right if you shine it on a red surface, since there's no red light to reflect off of it, screwing with the reflected color you see).

Combining 3 wavelengths, you can reproduce any color enclosed by the triangle that connects the 3 wavelengths. This is why RGB is good: it makes the biggest triangle, and reproduces the most colors, ie has the highest gamut. LCDs and such are not monochromatic light sources, hence why they can't go all the way to the edges, and the gamut is quite limited. Which is one reason that laser displays are a great idea: monochromatic light sources mean you get a wider color gamut!