Why does the beam end in the sky?

[grainde]

Could it actually be your viewing perspective relative to the beam. The closer you are to the source the shorter the distance to where your line of sight is aligned with the beam. ie you begin to look along the beam and so as the back scatter all comes back at essentially the same angle, at that point, the beam seems to terminate and slightly more brightly. As it heads out in to the atmosphere as well, there will be less particles and less scatter so this would account for the fact that the perceived brightness doesnt increase too greatly (theres also scatter of the scattered light returning, that would reduce its intensity too).

Blord's sky scraper photo also demonstrates barrel distortion created by a lens

 

[Cyparagon]

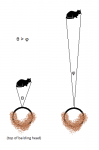
^that's pretty much what I illustrated.

which causes enhanced scattering of the laser beam back to your eyes. Above the PBL, which can be very low at night (<100 m), the amount of aerosols is very low compared to within the PBL, and as a result the scattering of the laser beam appears to end abruptly

Again I'll say: That would mean pointing at the horizon would make the beam much longer. That is not the case.

I'll try to draw something better...

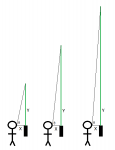
We do not see in length, we see in angles. That is why objects farther away look smaller - they take up less angle:

So lets just measure a laser beam as the angle of vision that it occupies (since that's what the op is asking about anyways) instead of the "actual length."

Say you were holding the pointer 2 feet away from you with an outstretched arm at eye level pointing directly upwards. A few hypotheticals (and a preview to calculus :shhh: ) - Let's assume zero divergence, and infinite atmosphere with no variation throughout. What if the laser actually stopped at 10 feet? What about 20? 30? What angle of our vision would be occupied?

If you'll recall from your trig class (and for those of you that haven't had trig, you'll just have to trust me ), the tangent of the angle θ is the length of the opposite side of the triangle divided by the length of the adjacent side of the triangle. In this case:

tanθ=Y/X

Taking the inverse tangent: θ=arctan(Y/X)
Since X is hypothetically 2: θ=arctan(Y/2)

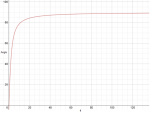
We find the answers for 10, 20, and 30ft to be 78.7°, 84.3°, and 86.2°
What about for 100 feet, 200 feet, or 300 feet? Those would be 88.9° 89.4°, and 89.6°

Do you see a pattern? This is where graphing comes in handy.

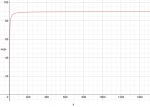
It seems to be approaching the number 90, no matter how long the laser gets. Let's zoom out further...

Which begs the question, could you even tell the difference between a 300ft beam and a 300-trillion foot beam? Not if it originates in your hand you couldn't. Not unless you had something to terminate the beam on for reference. That's the angular difference between 89.6° and 90°.

 

[Izord]

I call BS on the "Planetary boundry layer." Beams don't look any longer when you point them toward the horizon.

Thanks for the answers. I should have a 1400 mW blue laser next week to compare the beam length with my green laser.

Cyparagon seems to have a valid point. The beam ends the same distance (perceived effect, I know it continues into space) whether you point it up or at a shallow angle to the surface of the planet.

Has anyone compared different strengths of lasers, like 100mW vs 1000mW for how far away the beam seems to end?

Izord

 

[ElektroFreak]

@Cyparagon: Is your only reference that "that is not the case" your eyes? If so, then it's very hard to trust that over the references that have been presented here so far. With scientific topics, if one doesn't have verifiable firsthand experimental results obtained and verified using standard scientific method, then in order to obtain a valid explanation for a given phenomenon there are two options:

1) Create and execute an experiment using proper scientific method, and share your results with the professional scientific community. The results will then be validated by others who combined have a huge amount of experience and education..

2) Search for and consult any and all references on the topic, using the knowledge and experiences of others whose education or scientific experimentation has provided them with some sort of answer.

Science is not always 100% accurate. As a prime example, in physics the currently accepted model is wrong on some level. I say that with certainty because there are things that are yet to be understood in the physical universe. All we can do is create models that make the most sense and that adequately explain it using the knowledge we do have.

Regarding the topic at hand, when I vary the angle of a laser aimed at the sky I can't say for sure whether the visible portion of the beam changes length because the perspective from the ground anywhere near the source isn't a good vantage point. In fact, I'd say it would be difficult to get a good idea of what is happening from any vantage point except from a midpoint altitude, and then in order to have valid numbers one would need some good measuring equipment by my logic.

 

[Wolfman29]

It should be a pretty easily experiment. Take a camera, put it six inches to the left/right of the laser, use the same exposure settings, and take pictures of the beam pointing towards the horizon as well as pointing straight up. Get pictures, measure lines =p

 

[Izord]

Has anyone measured the perceived beam length? You could point it at a star then go 10 meters away, or 100 meters, then measure the angle from the star to the end of the beam.

Then repeat with a ground based object in the distance.

I will try to think of something to measure the angle with. Something a surveyor uses.

Then it's pretty simple geometry to determine the beam length.

I wonder if it depends on the power of the laser, or where you are on the earth.

 

[Izord]

It should be a pretty easily experiment. Take a camera, put it six inches to the left/right of the laser, use the same exposure settings, and take pictures of the beam pointing towards the horizon as well as pointing straight up. Get pictures, measure lines =p

That's even easier than what I said. Still be nice to have some numbers.

Found it, it's called a theodolite. Anyone know how to make one?

Now I remember I used to have a brunton compass that would do the job.

Darn, found the one I had when I used to do land navigating, but it only does horizontal, my pop had the one that would do vertical.

 

[ElektroFreak]

It should be a pretty easily experiment. Take a camera, put it six inches to the left/right of the laser, use the same exposure settings, and take pictures of the beam pointing towards the horizon as well as pointing straight up. Get pictures, measure lines =p

I'd wager the measurements made that way would be virtually identical to each other due to perspective.

 

[Wolfman29]

Well, isn't that what we're testing? Whether or not perspective plays a roll here?

 

[ElektroFreak]

You guys are, but I'm content with the established answers that others who are far more educated than I have already found via their experimentation and education. No need to reinvent the wheel.

 

[Izord]

You guys are, but I'm content with the established answers that others who are far more educated than I have already found via their experimentation and education. No need to reinvent the wheel.

I just want to know why the beam ends. If it's the same distance horizontall as vertical, that established answer about the aerosol layer may seem to be incorrect.

:thinking:

 

[ElektroFreak]

How has it been scientifically established here that the boundary layer theory may be inaccurate? It hasn't. Therefore I'm going with what the doctor at NASA says over any contesting point made in this thread. This is just common sense, business as usual when doing scientific research.

 

[Cyparagon]

Wow, I took a few minutes to add drawings, and there have been ten posts in that time.

Please see my edited post above.

Regarding the topic at hand, when I vary the angle of a laser aimed at the sky I can't say for sure whether the visible portion of the beam changes length because the perspective from the ground anywhere near the source isn't a good vantage point.

Precisely.

Obviously, if you could view a vertical beam from hundreds of miles away from the source, it would stop where the atmosphere stops. That isn't pertinent to pointers though. :beer:

 

[Izord]

Wow, I took a few minutes to add drawings, and there have been ten posts in that time.

Please see my edited post above.



Precisely.

Obviously, if you could view a vertical beam from hundreds of miles away from the source, it would stop where the atmosphere stops. That isn't pertinent to pointers though. :beer:

Thank you, very convincing. Those Brunton 'Transit' Compasses that can measure vertical angles start around $300.

I may have to make one with a protractor, string, and weight bob.

 

[ElektroFreak]

If that is more convicing to you than a reply from someone educated in the field, and who works with this phenomena directly its obvious to me that this dicussion is pointless. I fully support free thought, but here a question was asked, verifiable answers from qualified sources provided by at least 2 people, but still people with comparatively little qualifications insist on other explanations. Sometimes people make my head hurt..

 

[Benm]

I think there are two things going on here that are mixed up because their effects are similar when it comes to how something looks:

1 - there is the perpective issue, pronounced when you are close to the laser (e.g. handheld). You simply could not tell if the beam was 1 or 100 kilometers long from that vantage point.

2 - scattering. In order to see a beam, 2 things need to be accomplished: The beam needs to travel the distance at which you see it, AND the scattered light has to make it back to your eye in order to see it.

Point 2 is interesting, especially when you use lasers in dense fog. Even handheld, the beam seems to just stop at some distance from you. Depending on the density of the fog this can appear to be 10 meters to 100 meters or so.

Obviously the beam doesnt make a dead stop at 10 meters, it gradually loses power as the light is scattered. But it seems to make a very abrupt stop at some distance. This effect is caused by the scattered light becoming lower than the ambient light and almost invisible quickly after that distance.

Compare it to what you see when a car drives towards you on a foggy night: You will rather suddenly see the headlights and they will be very visible very quickly. It is not the very gradual buildup of intensity that you would see for a car with very weak lights coming towards you on a clear night at all.