phosphoressential
New member
- Joined
- Nov 11, 2018
- Messages
- 10
- Points
- 3
Hi All!
First real post. Real happy to be here.
This is something everyone thinks about at some point when dealing with what power you need to achieve a visual effect with a certain wavelength of light. What I would like to see is a graph of the milliwattage needed at any wavelength to achieve a "visible beam" in reasonably low lighting. I've never seen one, so I decided to go ahead and bang one out and get the idea going.
I would love any and all help to approve/improve/disprove any of the work i've done. Thanks!
First, my current results:
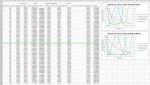
(Almost) Full Visible Spectrum

Zoomed for Resolution Blue to Yellow

The main two concepts I used were that our eyes are only so sensitive to a certain color, and only a certain amount of a certain color will escape the beam for us to perceive and see the beam.
I started with a plot of the human eye's sensitivity to different wavelengths (blue/right axis). Data was generated from http://www.cvrl.org/lumindex.htm, which purportedly gives the "CIE 'physiologically-relevant' luminous efficiency functions consistent with the Stockman & Sharpe cone fundamentals."
I then plotted the amount of light that will scatter from the beam when it is traveling through air (red/right axis). The true proportion of light that gets to our eyes from the beam is very small, so I normalized it to the visible spectrum in order to more easily graph it.
We then combine these effects by multiplication and normalize across the spectrum, and we get the purple (right axis) plot. This is the visibility of a light beam going through air (at a certain viewing angle) at different wavelengths. This shows us how different colors relate to each other at any certain power level. We now need to figure out what we mean by a "visible beam," and set a reference point. With the knowledge I have and some mild research, I decided to go with a standard 5mW 532nm green laser pointer. They are very common, considered safe for the general public with minimal precautions. They can also be seen reasonably well in a reasonably low lighting environment from most viewing angles.
To apply the sensitivity plot to the reference point and calculate the final plot, I took the reciprocal of the sensitivity, normalized it to the value at 530nm (close enough to 532), and multiplied it by 5, the power of our reference beam at 532. This produces the green plot (left axis), which supposedly shows the laser power needed for a beam to be as visible as a 5mW 532nm beam in the same conditions at any visible wavelength. From the limited research I've done, the numbers seem pretty reasonable. What do you think?
That's all I can think to say right now. What are other significant factors I should include? As far as I can think, LIV curves are inconsequential because we're talking about optical power. Feedback please!
Cheers! Happy lasing!
Nigel
First real post. Real happy to be here.
This is something everyone thinks about at some point when dealing with what power you need to achieve a visual effect with a certain wavelength of light. What I would like to see is a graph of the milliwattage needed at any wavelength to achieve a "visible beam" in reasonably low lighting. I've never seen one, so I decided to go ahead and bang one out and get the idea going.
I would love any and all help to approve/improve/disprove any of the work i've done. Thanks!
First, my current results:
(Almost) Full Visible Spectrum

Zoomed for Resolution Blue to Yellow

The main two concepts I used were that our eyes are only so sensitive to a certain color, and only a certain amount of a certain color will escape the beam for us to perceive and see the beam.
I started with a plot of the human eye's sensitivity to different wavelengths (blue/right axis). Data was generated from http://www.cvrl.org/lumindex.htm, which purportedly gives the "CIE 'physiologically-relevant' luminous efficiency functions consistent with the Stockman & Sharpe cone fundamentals."
I then plotted the amount of light that will scatter from the beam when it is traveling through air (red/right axis). The true proportion of light that gets to our eyes from the beam is very small, so I normalized it to the visible spectrum in order to more easily graph it.
We then combine these effects by multiplication and normalize across the spectrum, and we get the purple (right axis) plot. This is the visibility of a light beam going through air (at a certain viewing angle) at different wavelengths. This shows us how different colors relate to each other at any certain power level. We now need to figure out what we mean by a "visible beam," and set a reference point. With the knowledge I have and some mild research, I decided to go with a standard 5mW 532nm green laser pointer. They are very common, considered safe for the general public with minimal precautions. They can also be seen reasonably well in a reasonably low lighting environment from most viewing angles.
To apply the sensitivity plot to the reference point and calculate the final plot, I took the reciprocal of the sensitivity, normalized it to the value at 530nm (close enough to 532), and multiplied it by 5, the power of our reference beam at 532. This produces the green plot (left axis), which supposedly shows the laser power needed for a beam to be as visible as a 5mW 532nm beam in the same conditions at any visible wavelength. From the limited research I've done, the numbers seem pretty reasonable. What do you think?
That's all I can think to say right now. What are other significant factors I should include? As far as I can think, LIV curves are inconsequential because we're talking about optical power. Feedback please!
Cheers! Happy lasing!
Nigel